【中1数学】数直線の読み方と使い方｜正負の数を「位置」で理解する最初のステップ

導入

「−3って、0より小さいってだけでしょ？」「数字が大きい方が大きいんじゃないの？」
そんな誤解は、中1で正負の数を習い始めたときによく起こります。
実はこの理解の差は “数直線をイメージできるかどうか” で大きく変わります。
この記事では、正負の数を理解するための土台となる 数直線の読み方と使い方 をわかりやすく解説します。
ではさっそく見ていきましょう。

---

ポイント①：正の数・負の数は「位置」で決まる

数直線とは “数を一本の線の上に、位置で表すもの” です。

• 0を基準にして
• 右へ行くほど大きく
• 左へ行くほど小さくなる

たとえば、

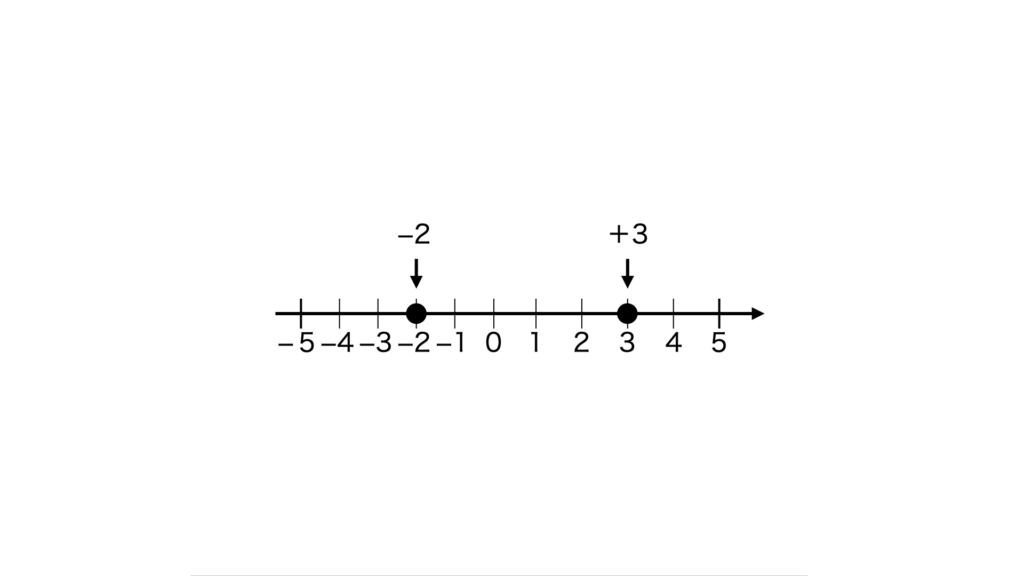
• ＋3 は「右へ3」
• −2 は「左へ2」

つまり、数は “どこにあるか” が意味そのもの なのです。

黒板まとめ

• 右＝大きい
• 左＝小さい
• 数は「位置」で考えるのが基本

---

ポイント②：数直線を使うと大小関係が一瞬でわかる

数字だけ見ると、＋5 と −5 は「見た目は同じ」。

しかし数直線では…

• ＋5 は右
• −5 は左

→ 右にある方が大きいので、＋5 の方が大きい。

数字の見た目ではなく
位置で比べるのが正負の大小関係のルール です。

---

ポイント③：差（距離）や移動のイメージが自然につく

数直線を見ると「どれだけ動いたか」がすぐにわかります。

例：
−2 から ＋3 へ移動する場合
左から右へ5つ分動くので、差は 5。

この「距離」の感覚がつくと、整数の計算が直感的に理解できるようになります。

---

よくある誤解

• ❌ 「−5の方が数字が大きいから大きいでしょ？」
  　→ 違います。右が大きい。−5は＋5より左です。
• ❌ 「＋と−は比べられないんじゃ？」
  　→ 比べられます。0をはさんだ位置で比較できるからです。

---

確認問題

問1

どちらが大きい？
＋3 と −1

クリックで答えを表示

【解説】
＋3は0より右、−1は左。
右の方が大きいので＋3。
【答え】＋3

---

問2

−4 から ＋2 へ動くと、何だけ動く？

クリックで答えを表示

【解説】
−4 から 0 までで4、0 から 2 までで2。
→ 合計 6つ分の移動。
【答え】6

---

問3

次のうち最も小さい数を選びなさい：
−1、−3、2

クリックで答えを表示

【解説】
最も左にあるものが一番小さい。
→ −3 が最小。
【答え】−3

---

まとめ

• 数直線は「数の位置」を表す道具
• 右＝大きい、左＝小さい
• 数の大小・差・移動をすべて位置で理解できる
• 正負の理解は数直線のイメージが土台になる

---

指導のコツまとめ

• まずは数直線を書かせて“位置の感覚”を定着させる
• 文字よりも「どっちが右か左か」を優先して考えさせる
• 差（距離）のイメージを必ず取り入れる
• 正負の大小比較を数直線で必ず確認させる
• 中1の早い段階で“位置の言語”を習得させると計算ミスが激減する

---

---