反比例のグラフはなぜ曲線？｜だんだん変化がゆるやかになる理由

---

はじめに：「比例は直線、反比例は曲線」の意味わかってる？

反比例を教えるとき、多くの教科書や指導書ではこう説明されています。

「反比例のグラフは原点を通らない曲線になります」

しかし、生徒の多くは「曲線＝そういうもの」としか理解していません。
なぜ曲線になるのか？比例との違いはどこにあるのか？
この“なぜ？”に答えられるようにしておくことが、理解の深さを左右します。

---

ポイント①：xが増えるとyは減る、けどそのペースがだんだん変わる

反比例の式

y = a ÷ x

では、xが増えるとyは確かに減っていきます。

でもポイントはここ：

xが1ずつ増えるとき、yの減り方はどんどんゆるやかになる

たとえば、a = 12 のとき：

x	y = 12 ÷ x
1	12
2	6
3	4
4	3
5	2.4
6	2

→ はじめは大きく減るけど、だんだん変化が小さくなる。

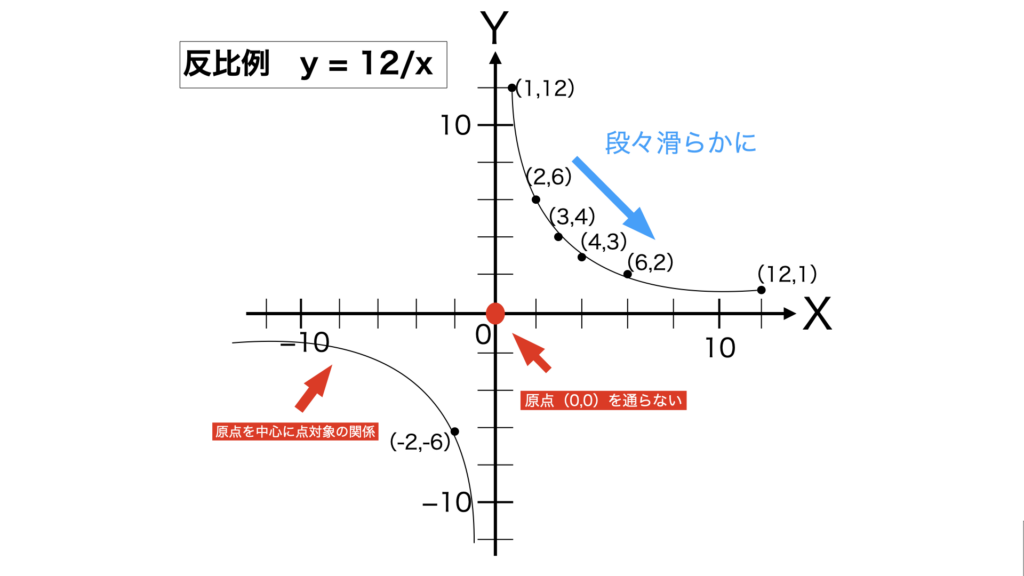
この「変化のスピードがどんどん変わる」という特徴が、グラフを“曲げる”理由です。

---

ポイント②：曲線は「傾きが変わっていく」グラフ

比例では、xが1増えるたびにyの増え方（傾き）が一定でした。だからグラフは直線。

でも反比例では：

• xが1→2：yは12→6（−6）
• xが2→3：yは6→4（−2）
• xが3→4：yは4→3（−1）

→ 右に進むほど、上下の変化が小さくなっていく

このように、傾きがどんどん変化していくので、線がまっすぐにならず、なだらかな曲線になるのです。

---

ポイント③：反比例の曲線は「地面にすべるような坂道」

生徒にとって、反比例のグラフはとっつきにくい印象があるかもしれません。
そこで伝え方として有効なのが、「反比例のグラフは、急な坂から地面にすべるように変化していく道」だとたとえることです。

• 最初は急に落ちる
• だんだん水平に近づいていく（でも地面にぴったりくっつくことはない）

こういうイメージをもたせると、グラフを描くことにも意味を感じられるようになります。

---

まとめ：曲線は「変化のスピードが変わる」証拠

反比例のグラフが曲線になるのは、xが増えるにつれて、yの変化のスピードがゆるやかになるから。
それはつまり、傾きが一定でないことの証拠です。

グラフは、関数の“変化の性格”がそのまま見た目に表れているもの。
比例＝直線、反比例＝曲線という形の違いにも、しっかりとした理由があります。