はじめに:「比例と何が違うの?」という第一の壁
中1で比例・反比例を学んだ後、次に出てくるのが「一次関数」。
このとき生徒がよく言うのが、
「y = ax なら比例でしょ?
y = ax + b は…何が違うの?」
ここでのつまずきを防ぐには、比例との「つながり」と「ちがい」の両方を視覚的に伝えることが大切です。
👉 本記事は 中学数学「関数」まとめ の一部です。比例・反比例・一次関数を体系的に整理した一覧はこちらから。
ポイント①:「y = ax + b」は原点を通らない(b≠0のとき)
まず押さえるべきは、
一次関数→比例の仲間だけど、スタートがズレてる
という位置づけ。
比例(y = ax)は常に原点(0,0)を通りますが、
一次関数(y = ax + b)は「スタート地点がy軸のどこか」にズレているだけです。
・y = 2x(比例)→ 原点からスタート、傾き一定
・y = 2x + 3(一次関数)→ 傾きは同じ、でもy軸では3から始まる
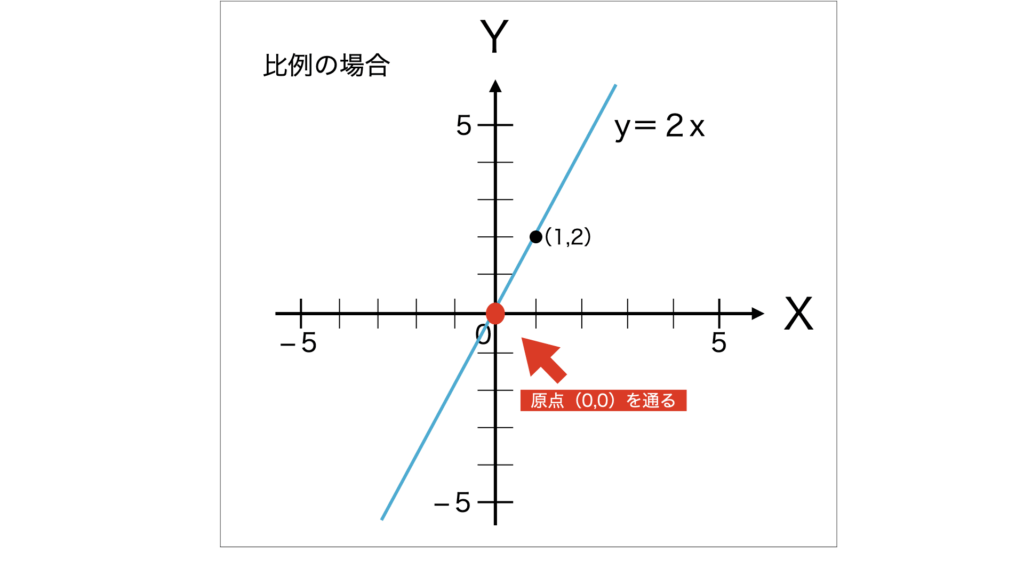

→ グラフの形はどちらも直線。ただし通る場所が違う。(x=0の時のyの値が違う)
比例では「xを2倍にするとyも2倍、xを3倍にするとyも3倍」という“倍々関係”が成り立ちます。
しかし、一次関数はスタートがずれている(+bがある)ため、この関係は成り立ちません。
例:
- y = 2x(比例)では、x=3→y=6、x=6→y=12 と、xが2倍になるとyも2倍。
- y = 2x + 3(一次関数)では、x=3→y=9、x=6→y=15 と、xが2倍になってもyは2倍にならない。
👉 つまり「一次関数は直線ではあるけれど、比例のように“倍々関係”を持つわけではない」というのが最大の違いです。
ポイント②:bの正体は「スタート地点の高さ」
bは、y軸とぶつかる高さ(y切片)を表します。
- y = 2x + 3 → y軸の「3」の位置からスタート
- y = -x – 4 → y軸の「−4」からスタートして、右下がりに進む
この「+b」のおかげで、どんな場所からでもスタートできる関数が作れるようになります。
つまり一次関数とは、比例に「自由なスタート地点」を加えたバージョンなんです。
ポイント③:「直線だけど原点を通るとは限らない」がカギ
生徒には「比例との最大のちがい」をこう伝えると分かりやすいです。
- 比例:原点を通る直線
- 一次関数:原点を通らないかもしれない直線
グラフがまっすぐならどちらも「直線の関数」ですが、
原点を通るかどうかが、比例と一次関数の分かれ道です。
まとめ:「比例+b」=一次関数という広がり
比例のようにまっすぐ進むけれど、bの値によってスタート地点がズレる。
それが一次関数です。
「比例をちょっと広げたもの」として一次関数を見せておくと、
生徒は「知らない世界」ではなく「続きの世界」として安心して入っていけます。
👉 本記事は 中学数学「関数」まとめ の一部です。比例・反比例・一次関数を体系的に整理した一覧はこちらから。





コメント